Geschichte der Algebra

Eine kleine Geschichte der Algebra ist erklärt die Herkunft des Begriffes und wie die wichtigsten Techniken der Algebra entstanden sind. Es ist mehrheitlich eine Kopie des Artikels von der Wikipedia ergänzt durch Links auf die Khan Academy. Schau sie dir an! Hoffentlich kannst du schon bald auf der Khan Academy Deutsch die Geschichte und Techniken der Algebra lernen!

Der Begriff Algebra stammt aus dem Titel des Rechen-Lehrbuchs Al-Kitāb al-muḫtaṣar fī ḥisāb al-ğabr wa-ʾl-muqābala („Das kurz gefasste Buch über die Rechenverfahren durch Ergänzen und Ausgleichen“, entstanden um 825) des persischen Mathematikers und Universalgelehrten al-Chwarizmi, der im 9. Jahrhundert in Bagdad wirkte. Vier Jahrhunderte nach der Publikation des Buches erschien seine lateinische Übersetzung Ludus algebrae almucgrabalaeque. Aus „al-ǧabr“ entwickelte sich das heutige Wort „Algebra“. Die Anfänge gehen jedoch noch viel weiter zurück !

Zeit der Babylonier

Bereits 2000 Jahre vor unserer Zeitrechnung waren die alten Babylonier in der Lage, Gleichungssysteme der Form

die äquivalent zu einer quadratischen Gleichung der Form sind, zu lösen. Solche Gleichungen können irrationale Zahlen als Lösungen haben. Die Babylonier interessierten sich jedoch nicht für exakte Lösungen, sondern berechneten, meist mit Hilfe linearer Interpolation, ungefähre Lösungen. Auch befassten sich die Babylonier noch nicht mit negativen Zahlen. Eine der bekanntesten Tontafeln der Babylonier ist Plimpton 322, die zwischen 1900 und 1600 vor Christus erstellt wurde. Sie listet pythagoreische Tripel, was bedeutet, dass die Babylonier bereits 1000 Jahre vor Pythagoras die Bedeutung dieser Zahlen kannten.

Zeit der Ägypter

Die Babylonische Algebra war weiter fortgeschritten als die Ägyptische Algebra der gleichen Zeit. Während die Babylonier sich mit quadratischen Gleichungen befassten, untersuchten die Ägypter hauptsächlich lineare Gleichungen.

Der Papyrus Rhind, eine der wichtigsten Quellen für das heutige Wissen über die Mathematik im Alten Ägypten, wurde um 1650 vor Christus von Ahmes aus einem älteren Werk übersetzt. In dem Papyrus werden lineare Gleichungen der Form und 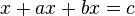, wobei a, b, und c bekannt sind und x die Unbekannte ist, mit geometrischen Methoden gelöst.

Zeit der Griechen

Ebenso wie die Ägypter und Babylonier untersuchten auch die alten Griechen algebraische Gleichungen. Jedoch waren sie nicht nur an praktischen Fragestellungen interessiert, sondern sahen insbesondere in den frühen Phasen geometrische Fragestellungen als zentrales Teilgebiet ihrer Philosophie. Dies war der Beginn der Algebra und der Geometrie und damit der Mathematik als Wissenschaft. Die Terme algebraischer Gleichungen repräsentierten bei den Griechen Seiten, meist Strecken, geometrischer Objekte. Mittels Konstruktionsverfahren mit Zirkel und Lineal bestimmten sie Lösungen bestimmter algebraischer Gleichungen. Da die altgriechische Algebra also durch die Geometrie begründet wurde, spricht man von der geometrischen Algebra. In jüngster Zeit ist diese Interpretation jedoch umstritten.

Der zweite Band der von Euklid verfassten Elemente enthält eine Reihe von algebraischen Aussagen, die in der Sprache der Geometrie formuliert wurden. Euklid diskutierte in den Elementen unter anderem die Theorie der Flächenanlegung, die auf die Altpythagoreer zurückgeht. Mit dieser Methode kann man aus Sicht der modernen Algebra bestimmte lineare und quadratische Gleichungen mit einer Unbekannten lösen. Im zehnten Buch der Elemente überlieferte Euklid einen Beweis der Irrationalität der Wurzel aus 2.

Diophantos von Alexandria, der wahrscheinlich um das Jahr 250 nach Christus lebte, gilt als der bedeutendste Algebraiker der Antike. Sein erstes und wichtigstes Werk, die Arithmetica, bestand ursprünglich aus dreizehn einzelnen Büchern, von denen aber nur sechs überliefert sind.^[9] Mit diesem Werk löste er die Arithmetik und die Algebra, was die Betrachtung positiver, rationaler Lösungen von Problemen angeht, vollständig von der Geometrie ab. Auch unterschied sich die Mathematik von Diophantos von der der Babylonier, denn er war primär an exakten und nicht approximativen Lösungen interessiert.